
Um breve tutorial
sobre matriz de
correlação no R
Uma matriz de correlação é uma ferramenta poderosa no entendimento das relações entre variáveis e é fundamental que faça parte de suas análises exploratórias. Apresentaremos nesse breve tutorial um pouco da teoria por trás da matriz de correlação sem entrar em detalhes matemáticos e como construir uma forma de visualizar essa matriz.
Primeiramente é importante definir o que é uma correlação. De forma geral, correlação é uma associação estatística comumente referida como o grau pelo qual um par de variáveis estão linearmente relacionadas. Se duas variáveis têm uma correlação positiva, significa que o aumento de uma é acompanhado pelo aumento da outra. Já uma correlação negativa significa que a diminuição de uma é acompanhada pelo aumento da outra e vice-versa. Quando uma variável não apresenta uma correlação linear com outra variável, a correlação é zero. Isso geralmente acontece quando são observados dois eventos aleatórios independentes. Os valores de correlação vão de -1 até +1.
“CORRELAÇÃO É QUALQUER RELAÇÃO ESTATÍSTICA, SEJA ELA CAUSAL OU NÃO, ENTRE DUAS VARIÁVEIS.”
É importante entender que o número apresentado na correlação não diz a intensidade do efeito do crescimento de uma variável na outra, ou seja, uma correlação com número absoluto maior não quer dizer vai gerar mais crescimento na outra.
A figura a seguir mostra alguns possíveis valores de correlação e exemplos de como podem ser os gráficos de dispersão entre essas variáveis. Vemos pela segunda linha de exemplos que, independente da intensidade do crescimento (ou diminuição), a correlação é indicada pelo mesmo número, assim o número indicado pela correlação indica a qualidade da relação entre as variáveis, o quão perfeito é o impacto do crescimento de uma variável na outra.

Outro ponto importante é uma das limitações da correlação: ela consegue enxergar apenas relações lineares. Pode-se ver que há exemplos de duas variáveis que claramente apresentam padrões, mas a correlação apresentada é nula.
Agora que cobrimos o entendimento da unidade básica da matriz de correlação, vamos entender o que é essa matriz.
Ao fazer uma análise de dados, normalmente temos várias variáveis que precisaremos analisar qual a correlação entre elas. Tentar observar a correlação de cada par manualmente, criando a correlação de cada um desses pares é uma tarefa morosa e pouco produtiva. A matriz de correlação permite que a correlação de todos os pares de variáveis possa ser observada em uma tabela.
Isso pode ser feito de maneira muito simples nas principais ferramentas de análise de dados de hoje. Como demonstração, vamos apresentar como isso pode ser feito em R.
Para isso, usaremos de exemplo a base de dados mtcars que já vem embutida na instalação básica do R, assim você pode fazer no seu computador, e a biblioteca corrplot, que pode ser instalada através do comando install.packages. Antes de gerar a matriz de correlação, vamos verificar como são os dados dessa base vendo as primeiras linhas.
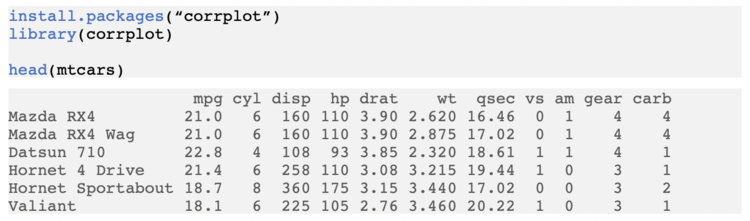
Para criar uma matriz de correlação que faça sentido, é importante entender o que cada variável significa:
mpg: milhas por galão
cyl: número de cilindros
disp: Displacement (cu.in.)
hp: cavalo-força
drat: razão do eixo traseiro
wt: peso em libras
qsec: tempo para percorrer ¼ de milha, em segundos
vs: Tipo de motor (Tipo V = 0, reto = 1)
am: Tipo de transmissão (1 = automática, 0 = manual)
gear: Número de marchas (não incluída a marcha ré)
carb: Número de carburadores
Para efeito de ilustração, utilizaremos as variáveis das colunas 1 a 7, com exceção da variável “drat”. É importante selecionar apenas as variáveis que fazem sentido o entendimento da correlação. Lembre que correlação não gera causalidade, então tentar entender a correlação de duas variáveis que claramente não tem efeito uma sobre a outra pode ser perda de tempo.
Para criar a matriz de correlação, vamos fazer um subset do nosso datatrame original e a função cor(). Criaremos uma variável para receber essa matriz:
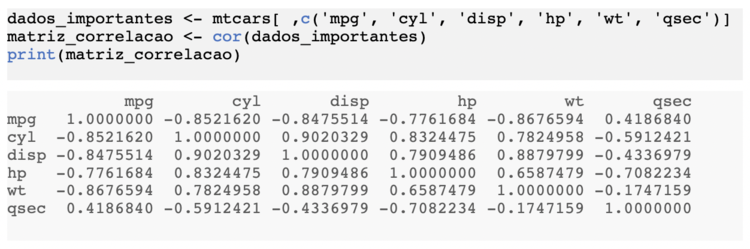
Com isso você chega na informação desejada: todas as correlações de todos os pares de variáveis. No entanto, visualmente não é agradável fazer essa análise. Para isso, vamos criar um correlograma, que é uma forma gráfica de visualizar essa matriz. Para isso, dentro da mesma biblioteca, tem a função corrplot().
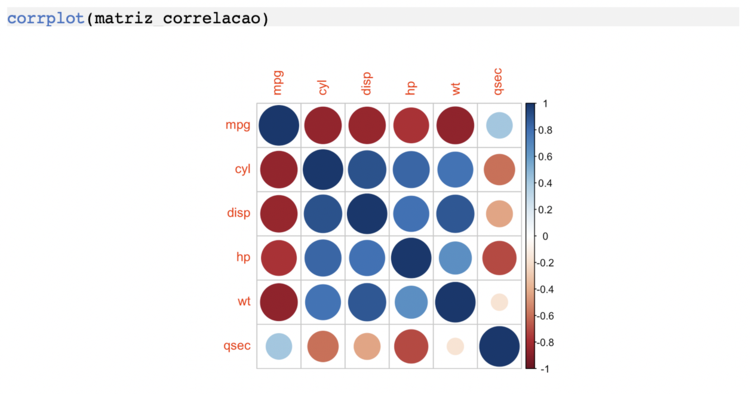
Esse é o gráfico padrão da função corrplot. Tanto o tamanho do círculo indica o valor absoluto da correlação, ou seja, quanto maior, mais próximo dos extremos. A intensidade da cor segue a legenda lateral. Essa é uma forma muito mais fácil de visualizar as correlações entre as variáveis.
A função ainda permite algumas configurações para deixar o gráfico mais personalizado. Aqui na numera gostamos de usar tons de azul e cinza, pois além de enxergarmos as diferenças, são mais amigáveis a alguns tipos de daltonismo. Faremos outras mudanças para conseguirmos focar nossa atenção na informação importante e facilitar a extração de insights.

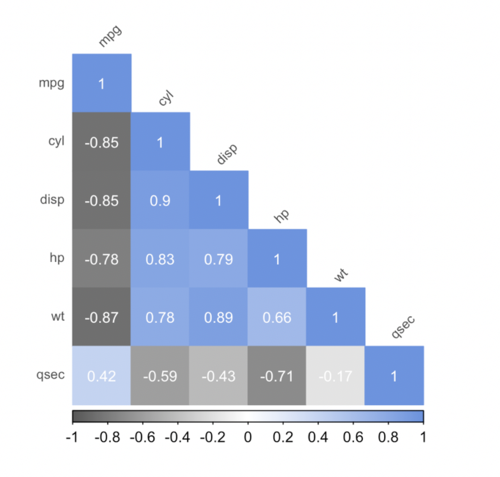
Com esse gráfico, que contém as mesmas informações da tabela da matriz, conseguimos rapidamente perceber que a variável “mpg” tem uma correlação forte e negativa com as variáveis “cyl”, “disp”, “hp” e “wt”. Vemos também que “cyl”, “hp” e “wt” são fortemente correlacionadas entre si e que “qsec” se correlaciona bem com “hp”, mas que as demais variáveis não têm correlação tão forte.
Com isso cumprimos o objetivo desse tutorial, que era entender o que é uma matriz de correlação, como construir e como visualizar. Você viu que, apesar de ser uma ferramenta de grande poder analítico, o gráfico de correlação pode ser criado com apenas algumas linhas de código. É uma excelente ferramenta para se ter à disposição para suas futuras análises. Espero que, com isso, tenha entendido os conceitos e aprendido como criar seu próprio correlograma.
Quer tentar fazer o seu? Segue aqui uma base de dados para você treinar:
https://www.kaggle.com/rhuebner/human-resources-data-set/download
Qualquer dúvida, entre em contato conosco através de nossos canais.
NARUHIKO HAMA
Entre em contato com a numera, será um prazer falar com você.
AV ÁGUA VERDE 1413, CURITIBA | RUA ALAGOAS, 1460 , BELO HORIZONTE

