Seus resultados fazem sentido?

Fique atento ao
que está por trás
de seus dados
Nossas decisões podem ser muito mais acuradas quando são embasadas por dados. No entanto, se eles não forem analisados corretamente, também podem nos fazer tomar decisões ineficazes. O objetivo deste artigo é introduzir o conceito chamado Paradoxo de Simpson e mostrar como esse paradoxo, relacionado à omissão de variáveis, pode ser prejudicial para nossas análises.
Imagine uma empresa do ramo de mineração, em que parte de seus funcionários estão muito expostos ao risco de acidentes de trabalho relacionados à extração de minérios . Para diminuir esse risco, a empresa oferece internamente treinamentos de segurança com o objetivo de orientar seus funcionários sobre as melhores práticas e técnicas mais seguras de exercer suas respectivas funções. Para analisar a eficácia desses treinamentos, o primeiro passo seria entender qual a relação entre a quantidade de horas que seus funcionários gastam em treinamentos de segurança e a quantidade de acidentes de trabalho que cada um deles sofreu em um determinado período de tempo.
Utilizando o software estatístico R, veremos essa análise graficamente (DICA: O pacote ‘ggplot2’ do R é uma excelente ferramenta para visualizações gráficas. Para mais informações sobre este pacote acesse este material.) Ao plotarmos a quantidade de horas de treinamentos de segurança e a quantidade de acidentes de cada funcionário, a reta de regressão (“geom_smooth”) indica a tendência entre essas duas variáveis, ou seja, o que acontece com o número de acidentes à medida que aumenta a quantidade de horas de treinamento.

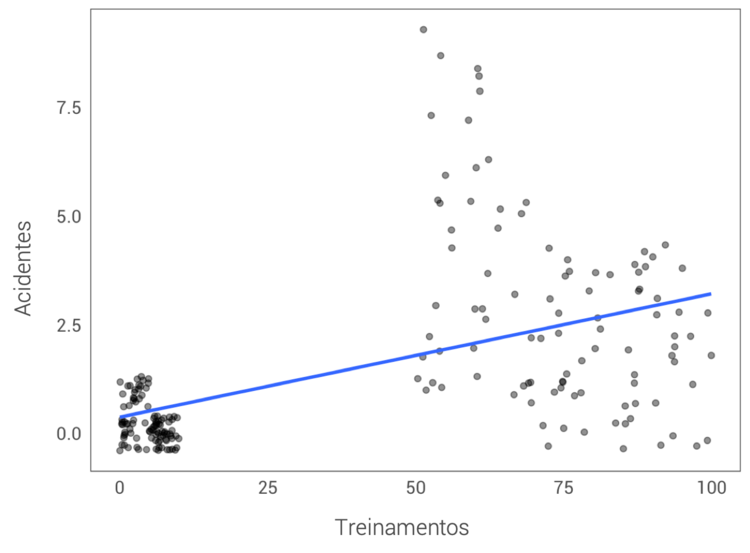
O gráfico revela que existe uma relação positiva entre a quantidade de horas de treinamento e o número de acidentes. Uma vez que quanto mais tempo de treinamento de segurança o funcionário possui maior é a tendência de sofrer um acidente, a conclusão mais óbvia seria pensar que o treinamento não está sendo eficaz para evitar acidentes e que, na verdade, ele poderia estar piorando a situação. Mas será que essa conclusão faz sentido? Parece bastante contra intuitivo, uma vez que o objetivo dos treinamentos de segurança é justamente fazer com que os funcionários exerçam seu trabalho com mais segurança e, consequentemente, reduzir o número de acidentes de trabalho.
FALÁCIAS ECOLÓGICAS – O QUE SÃO
Antes de voltarmos a esse exemplo, vamos entender o chamado Paradoxo de Simpson que é parte de um conceito chamado de ecological fallacy ou falácia ecológica, descrito por W. S. Robinson em um artigo chamado “Ecological Correlations and the Behavior of Individuals”, publicado na American Sociological Review em 1950. Falácias ecológicas são interpretações estatísticas de dados em que inferências sobre a natureza individual são deduzidas a partir de um grupo ao qual o indivíduo pertence.
“FALÁCIA ECOLÓGICA É O TERMO ASSOCIADO AO ATO DE DEDUZIR QUE AFIRMAÇÕES FEITAS À NÍVEL AGREGADO TAMBÉM SÃO VÁLIDAS À NÍVEL DESAGREGADO”
Um exemplo de falácia ecológica é o Paradoxo de Robinson – deduzir correlações de um grupo a partir de correlações populacionais. Em 1950, Robinson encontrou que quanto a maior a proporção de imigrantes de um estado americano, menor era a taxa de analfabetismo. Podemos dizer que os imigrantes são mais alfabetizados do que os não imigrantes? Em seu estudo, Robinson mostrou que a nível individual, em média, os imigrantes são menos alfabetizados do que os nativos e que há uma tendência deles se estabelecerem em estados com maior média de população nativa alfabetizada.
Para o propósito deste artigo, focaremos na falácia conhecida como Paradoxo de Simpson.
PARADOXO DE SIMPSON – CONCEITO E RELEVÂNCIA
O paradoxo de Simpson é um fenômeno em probabilidade e estatística no qual uma mesma tendência aparece em vários grupos de diferentes tamanhos dentro de uma amostra de dados, mas desaparece ou é revertida quando esses grupos são agregados. Estatísticos também chamam esse fenômeno de viés de variável omitida, ou seja, quando deixamos de levar em consideração o grupo ao qual pertencem as subpopulações de nossa amostra, podemos chegar a resultados enviesados. Você pode ler mais sobre viés de variável omitida e paradoxo de Simpson clicando aqui.
Esse fenômeno ocorre porque quando fazemos análises de médias, tanto o tamanho relativo dos grupos quanto os valores relativos dentro desses grupos influenciam no resultado final. O exemplo mais famoso desse fenômeno, envolve o processo de admissão de candidatos de pós-graduação na Universidade de Berkley, nos Estados Unidos. A média de candidatos homens aceitos nos programas de pós-graduação era maior que a média de candidatas mulheres. Mas, na realidade, o fato era que a grande maioria das mulheres se candidatavam para departamentos mais concorridos, e nesses departamentos específicos a média de mulheres aceitas era maior que a média de homens aprovados. Portanto, a omissão da variável departamento na análise inicial, distorce as diferenças nas médias de aceitação de candidatos por gênero na Universidade. Para saber mais sobre este estudo, clique aqui.
Voltando ao nosso exemplo inicial, o que aconteceria com nossa análise da empresa de mineração ao incluirmos a gerência a qual cada funcionário pertence? O mesmo gráfico anterior agora assume a seguinte forma:


Podemos ver que as retas que representam as tendências entre a quantidade de horas de treinamento e número de acidentes para todos os departamentos seguem em direção oposta à reta representada pelo gráfico 1 que é referente à análise agregada. Os funcionários da gerência A, que possui o maior número de acidentes de trabalho, provavelmente também são os funcionários que possuem maior quantidade de horas de treinamento. A gerência A pode estar associada a um trabalho de campo, mais exposto ao risco de acidentes e por isso participam de mais treinamentos. Já as gerências B e C podem estar relacionadas a trabalhos de backoffice, pois possuem poucas horas de treinamento e estão menos expostas à acidentes.
A gerência que possui mais horas de treinamento também possui o maior número de funcionários que sofreram acidentes de trabalho. Portanto, quando a comparamos com as outras que tem menor exposição ao risco, a média de acidentes por hora de treinamento aumenta. Isso implica dizer que analisar essas três gerências de maneira agregada torna nossa análise enviesada. Podemos considerar a variável gerência como uma variável de confusão, pois ela distorce nossos resultados quando não incluída na análise.
Para avaliar a eficácia dos treinamentos de segurança, uma série de outras variáveis devem ser levadas em consideração, como por exemplo o cargo, tempo de experiência, variáveis demográficas e até mesmo variáveis comportamentais de cada funcionário, para tentar isolar o efeito do treinamento em si.
“ANÁLISES SUPERFICIAIS JUNTAMENTE COM A OMISSÃO DE VARIÁVEIS PODEM NOS LEVAR A CONCLUSÕES PRECIPITADAS E QUE REPRESENTAM UM DISTORÇÃO DA REALIDADE QUE GOSTARÍAMOS DE MEDIR.”

COMO AVALIAR?
Na área acadêmica, um dos métodos mais utilizados para avaliação de impacto de uma intervenção, como o caso de um treinamento, é a realização de um experimento com aleatorização da intervenção. Esse método consiste na criação de dois grupos de análise, um grupo de controle e um grupo de tratamento, escolhidos aleatoriamente, que possuam as mesmas características e a única diferença – idealmente- seria que o grupo de tratamento passou pelo treinamento e o grupo de controle não. Dessa forma, é possível comparar os resultados dos dois grupos e a diferença entre eles será justamente o impacto do treinamento. O Itaú Social possui um curso de avaliação de impacto bastante conceituado na área acadêmica e seu material pode ser acessado pelo link.
Pode não ser surpresa que em nosso exemplo inicial, os treinamentos não estariam aumentando o número de acidentes de trabalho, mas o Paradoxo de Simpson pode estar presente em qualquer análise estatística e os resultados não serem tão óbvios assim. Caso sua empresa esteja fazendo análises de turnover, para investigar associações como médias de hora extra e pedidos de demissão, por exemplo, busque fazer tanto análises agregadas quanto por diferentes níveis hierárquicos como diretorias, gerências, cargos, etc. Essas análises separadas servem como base de comparação e podem trazer insights mais precisos. Caso queira conhecer mais sobre este tipo de análise, clique aqui e entenda por que os funcionários deixam suas empresas.
AMANDA GENTIL
FICOU INTERESSADO EM SABER MAIS?
Para maiores detalhes sobre o Paradoxo de Simpson e suas formalizações matemáticas, seguem alguns artigos interessantes.
Quer ajuda para fazer estas investigações internas na sua empresa? Entre em contato com nosso time de consultoria.

