Você tem interpretado seus resultados corretamente?

Extraia mais de
seus dados com a
ajuda do teorema
de bayespeople analytics
No dia a dia sempre lidamos com probabilidades, como as chances de chover, de pegar trânsito, ou de chegar a tempo no trabalho. E vamos ajustando essas probabilidades de acordo com novas informações que recebemos, por exemplo: se a chance de chover de acordo com um aplicativo é de 30% e você vê o céu fechar logo antes de sair de casa, você ajusta mentalmente essa probabilidade para um número maior e a decisão por sair de casa com o guarda-chuva se torna mais razoável. Isso é uma forma simples de aplicar o teorema de Bayes, que pode ajudar não só numa melhor predição de eventos, mas também ajuda a interpretar melhor os resultados de alguns exames. Com esse texto você irá entender o que é o teorema de Bayes, tanto na sua definição formal quanto nas suas aplicações práticas na vida e no contexto corporativo, além de entender como podem ocorrer erros de análise de probabilidade.
Suponha que você foi fazer um check-up de rotina e dentre os vários resultados apareceu um resultado positivo para uma doença incomum, onde apenas 1% da população tem a doença. Além disso, o médico diz que o exame tem uma acurácia alta, acertando em 99% dos casos.
COMO VOCÊ SE SENTIRIA FRENTE À ESSAS INFORMAÇÕES?
Situações como essa são comuns no nosso dia a dia, nos mais diversos espectros da nossa vida, e todas elas apresentam uma forma de lidar com novas informações de forma tão natural que acabamos nem percebendo. O teorema de Bayes fala exatamente sobre a forma como atualizamos nossas expectativas a partir de novas informações disponíveis.
“O TEOREMA DE BAYES DESCREVE A PROBABILIDADE DE UM EVENTO, BASEADO EM UM CONHECIMENTO A PRIORI QUE PODE ESTAR RELACIONADO AO EVENTO. O TEOREMA MOSTRA COMO ALTERAR AS PROBABILIDADES A PRIORI TENDO EM VISTA NOVAS EVIDÊNCIAS PARA OBTER AS PROBABILIDADES A POSTERIORI.”
— WIKIPEDIA
A definição matemática do teorema de Bayes é:

Apesar de parecer uma aplicação pouco provável no dia a dia, um exemplo simples pode mostrar como usamos o teorema de Bayes corriqueiramente.
Considere que numa mesa há duas caixas, uma cinza e uma azul. 10 bananas e 10 maçãs foram distribuídas nelas, mas você não sabe como foi a distribuição. Então, se for pedido que você tire uma fruta da caixa azul, qual a probabilidade de você tirar uma banana?
Sem nenhum conhecimento prévio o melhor chute seria 50%, já que a divisão das frutas é de 50% banana e 50% maçã. Mas com a informação de que na caixa azul têm somente bananas e na caixa branca têm somente maçãs, facilmente é possível atualizar essa probabilidade para 100%.
Dessa forma bem intuitiva aplicamos o teorema de Bayes sem usar nenhuma fórmula.
APLICAÇÃO GERAL

Vamos voltar ao nosso exemplo inicial, o diagnóstico de uma doença.
O teste possui uma precisão de 99%, o que nos leva a crer que qualquer indivíduo que tenha recebido positivo no teste tenha 99% de chance de ter a doença. No entanto, o médico forneceu uma segunda informação: apenas 1% da população tem essa doença. Vamos verificar como isso deveria mudar a forma de encarar os resultados.
Nesse caso, queremos verificar qual a probabilidade de a pessoa estar realmente doente dado que o teste detectou a doença.
Substituindo os dados na fórmula fica mais fácil entender:

– O teste detectar a doença dado que a pessoa é doente multiplicado pela possibilidade de se encontrar uma pessoa doente ao acaso;
– O teste detectar a doença dado que a pessoa não é doente multiplicado pela possibilidade de se encontrar uma pessoa saudável ao acaso.
Aplicando então a fórmula na situação:

Com isso descobrimos que na verdade, apesar da acurácia de 99% do teste, uma pessoa comum tem na verdade apenas 50% de chance de realmente ter a doença.
Talvez todo esse conceito ainda esteja muito abstrato para você. Uma forma de entender melhor o cenário é visualizar todos os passos desse cálculo separadamente. A figura abaixo nos auxilia nesse entendimento:
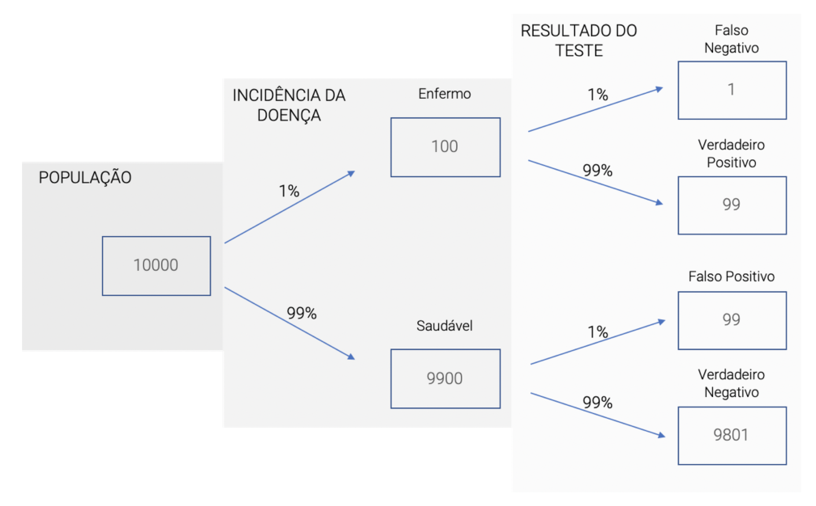
Considere 10.000 pessoas selecionadas aleatoriamente. Teremos 1% de incidência da doença, ou seja, apenas 100 das 10.000. Como o teste tem 99% de acurácia, dos 100 doentes, ele identificará corretamente 99 casos e 1 deles não será identificado.
O mesmo vale para pessoas saudáveis. Das 9.900 saudáveis, 1% ele identificará erroneamente como doente, ou seja, 99 serão identificadas como falso positivos.
Então se o teste deu positivo – há 198 casos em que isso acontece – metade deles é falso positivo e metade é verdadeiro positivo. Portanto, 50% de chances de o indivíduo estar realmente com a doença detectada.

CONSEQUÊNCIAS DE NÃO SE TER UMA HIPÓTESE A PRIORI
Para o caso de detecção de um falso positivo, pode-se imaginar que não existem consequências relevantes, afinal é “apenas” um falso alarme. No entanto, um estudo realizado nos Estados Unidos que acompanhou mulheres que passaram por teste preliminares de câncer de mama mostrou que as mulheres que tiveram resultado falso positivo tiveram maior chance de desenvolver câncer de mama nos 10 anos seguintes quando comparadas com as mulheres que tiveram resultado verdadeiro negativo. O aumento da incidência dependia dos testes confirmatórios utilizados. Quando era apenas uma radiografia, o aumento era de 39%, mas quando era feito uma biópsia, a chance de a mulher desenvolver o câncer aumentou em 76%. Portanto, para uma mulher jovem, saudável, sem histórico de câncer na família, a recomendação é que não se realize testes sem necessidade. Nesse caso, a falta de uma hipótese para se aplicar o teste apenas gera ruídos para as análises e ainda pode aumentar as chances de se desenvolver uma enfermidade.
(Henderson, L. M., Hubbard, R. A., Sprague, B. L., Zhu, W., & Kerlikowske, K. (2015). Increased Risk of Developing Breast Cancer after a False-Positive Screening Mammogram. Cancer Epidemiology Biomarkers & Prevention, 24(12), 1882–1889.)
APLICAÇÃO EM PEOPLE ANALYTICS
Pense agora num contexto mais corporativo onde resolveu-se investigar a correlação entre performance e a faculdade de origem dos colaboradores. Analisando os colaboradores com baixo desempenho (os 5% com os piores desempenhos), afirmou-se que 60% deles vinham da universidade X, e por isso deveriam excluir currículos de candidatos que viessem dessa universidade.
O problema dessa afirmação é que ela foi feita como se fosse uma análise preditiva, mas na verdade ela é uma análise descritiva e remete a um erro comum em que o analista confunde a probabilidade de pessoas serem da universidade X dado que elas têm baixo desempenho com a probabilidade de pessoas terem baixo desempenho dado que são da universidade X.
Para corrigir a afirmação feita, vamos primeiro entender como se chegou a essa conclusão. Para completar os dados, faremos a suposição de que entre os colaboradores que têm bom desempenho 40% não são da universidade X. Com isso conseguimos descrever a atual situação dos colaboradores da empresa.

Provavelmente se chegou na conclusão a partir da ramificação superior desse diagrama. Uma aplicação do teorema de Bayes nesse caso é assumir que essas são as informações a priori. Para descobrir as informações a posteriori, vamos tentar descobrir qual a probabilidade de o candidato ter um baixo desempenho dado que é da universidade X.
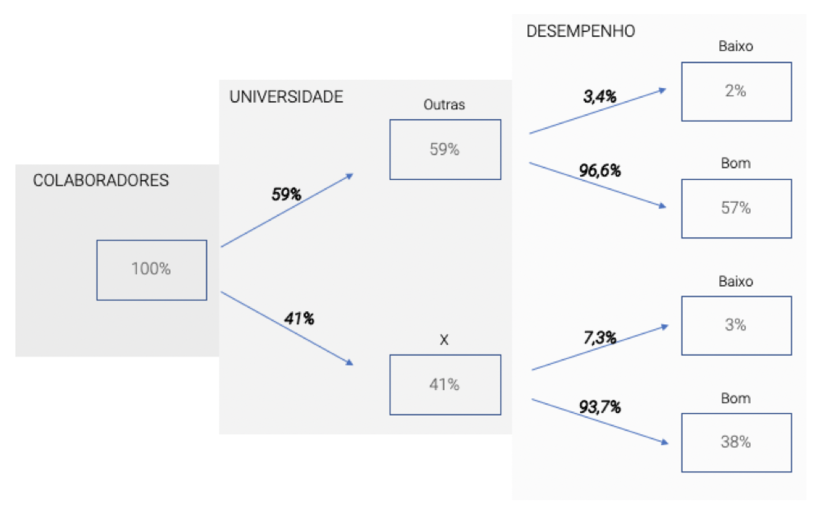
Preenchendo uma segunda árvore de probabilidades com exatamente os mesmos dados da árvore anterior, mas de forma reorganizada, vemos que, na verdade, apenas 7% daqueles que vem universidade X são de baixo desempenho. Então excluir os candidatos que vêm dessa universidade pode ser uma decisão precipitada.
De forma geral, para melhorar suas análises e tomada decisões lembre sempre de levantar hipóteses. Não realize testes sem motivos, pois eles podem acabar criando ruídos e levando a sua análise para a conclusão errada. Tente entender os mecanismos por trás das hipóteses quando for possível, pois isso torna mais claro a forma de validar os resultados.
Quer ajuda para fazer estas investigações internas na sua empresa? Entre em contato com nosso time de consultoria.

